-
Rupture plutôt profonde par
poinçonnement
-
tangent à la base de la couche
molle si celle-ci n’est pas trop épaisse
-
pour F # 1, fluage du
sol tassement anormal +
renflement du sol en pied de talus
-
Détermination du coefficient de
stabilité N
-
-
Puis en fonction de φ et du
rapport D/H, détermination du coef. de sécurité F
sur abaque (Pilot et Moreau)
-
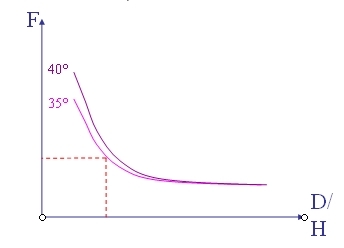
-
Si coef. de sécurité
insuffisant, solution de montée par phase, avec attente entre
chaque phase et possibilité de banquettes provisoires de
renfort
allongement du temps de réalisation de
l’ouvrage et des coûts
-
A chaque phase, le sol se consolide un
peu plus, donc Cu augmente donc le coefficient de stabilité N
augmente
-
cu = σ
x tg λ
La stabilité
d’un remblai se calcule de façon classique avec les
méthodes de calcul à la rupture en utilisant les
paramètres court terme du sol mou. La méthode de Bishop,
en circulaire a permis de construire de nombreux abaques
correspondant à des géométries variées. (Pilot
Moreau, 1973) Ces abaques ont été très utilisés
mais la diffusion des ordinateurs marque leur abandon. Mais aussi
bien pour ces calculs à la rupture que pour l’usage des
abaques, une correction proposée par Bjerrum et Pilot sur la
cohésion, est à apporter en fonction de l’indice de
plasticité. (Pilot, 1976) (Bjerrum, 1972) (fig
7-2)
L’anisotropie
des dépôts doit être aussi considérée.
Elle n’a cependant pas l’importance que l’on
croyait. Skempton (1964) quantifie le rôle de cette
anisotropie. Soit le rapport d’anisotropie K = C h
/ C v. Lors d’une rupture par cisaillement
Skempton postule que l’angle du plan de cisaillement avec les
directions principales est une constante de valeurs
(p/4
- j’/2). Il montre aussi que pour un angle i
par rapport aux directions principales de cohésion, cette
dernière s’exprime C i = C h ( 1 -
a sin2 i) ( 1 - b sin2 2i) avec a
= 1 - 1/K et b un facteur déformant de l’ellipse de
cohésion compris entre -0.1 et 0.1. Dans les programmes de
calcul, le plan de rupture est connu par l’angle a, par
rapport à l’horizontale. La formule
devient :
C
(a) = C
h ( 1 - a sin 2 ( - a - j )) (
1 - b sin 2 2(a - j))
Si l’on
connaît l’accroissement des pressions interstitielles
consécutives à la mise en place du remblai, un calcul en
contraintes effectives peut être fait. Mais cette connaissance
est délicate et l’usage de calculs aux
éléments finis est nécessaire. Cependant comme les
lois de comportement sont mal connues les résultats sont
délicats à interpréter. Pour palier à cette
insuffisance, la mesure des pressions interstitielles pendant la
construction d’un remblai est une très bonne
décision qui permet de caler un modèle de comportement et
surtout de prévenir une rupture. Avec les moyens actuels de
mise en place des matériaux les cadences sont très
élevées et la diffusion des surpressions interstitielles
n’est pas toujours assez rapide. Les mesures permettent de
construire la courbe de la figure 7-3. La partie AB de la courbe
correspond à la mise en équilibre statique de l’eau
dans le sol mou, la partie BC correspond au report des charges sur
l’eau, alors que la partie CD montre qu’une rupture est
en train de se produire, puisque les pressions augmentent plus vite
que la charge il y a donc cisaillement en cours.
A partir de
l’analyse de plus de trente cas de remblais bien
instrumentés, Tavenas et Leroueil, 1980, ont montré
que :
La très grande
majorité des dépôts argileux sont surconsolidés
et donc caractérisés par une rigidité
élevée en début de chargement.
Cette
surconsolidation, au début du chargement invalide
l’hypothèse de comportement non drainé, qui ne se
vérifie qu’a un certain stade du
chargement.
Ceci va permettre
une interprétation fiable des chemins de contraintes et de
proposer une méthode empirique fiable d’évaluation
des déplacements horizontaux sous les remblais.
 1. Sol mou
1. Sol mou

