L'arithmétique d'image regroupe toutes les
opérations d'image par image. Cependant ces opérations ne
peuvent se faire que sur des images de même
résolution.
On peut soit faire l'opération d'une image
quelconque par une image unie qu'on appellera une constante, soit
faire une opération d'image par image qui regroupe
l'addition, la soustraction, la multiplication, la division
...
Opérations algébriques du modèle
LIP
Pour f et g des fonctions en ton de gris de chaque
image, définies sur un compact D du plan et à
valeur réelle sur [0, M] (avec M>0, M=255 sur
l’échelle des niveaux de gris). Le niveau de gris
d’un pixel (i,j) est défini
par :
En traitement d’image on est souvent
amené à ajouter deux images dont leur radiosité
varie de 0 à 255. Si on part de deux images de
radiosité 200 et 205, on voit que ajouter ces deux images ne
peut être la somme des radiosités car le niveau de gris
vaut au plus 255. Ce qui conduit à la définition
d’une nouvelle loi d’addition des images appelée
addition LIP qui se définit comme
suit :
Pour f et g des fonctions en ton de gris de chaque
image, définies sur un compact D du plan et
à valeur réel sur [0, M]
L’ensemble des fonctions définies sur D
et à valeurs dans l’ensemble des tons de gris]- ∞,
M [est
notéG.
Par extension on défini la
soustraction LIP par :
Puis la multiplication LIP
L’ensemble G muni de l’addition LIP et
de la multiplication externe est un espace
vectoriel.
La nécessité de segmenter les images par
la recherche de contours donc de gradients
élévés à entraîné la définition
du contraste LIP.
Contraste LIP
Classiquement le contraste entre deux points
quelconques px et py de niveau de gris f(x) et f(y) se
défini par la relation:
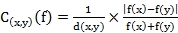pour
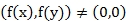
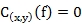sinon
Dans le cadre du modèle LIP, la notion de
contraste s’appuie sur un voisinage qu’il faut
définir au préalable.
Le contraste entre deux points x et
y d’une image s’obtient par la relation
suivante:
Ou encore
Avec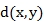 
la distance
Euclidienne entre x et y
Plutôt que de se limiter au cas de deux
points, étendons cette définition à un ensemble xi
de points voisins du point x.
Le contraste en un point x est défini
par :
Avec xi les pixels voisins de x et n le nombre de
voisins prise en
compte.
Il faut donc dans un premier temps définir un
voisinage sur lequel on va évaluer le minimum et le maximum du
niveau de gris puis la distance Euclidienne entre le pixel courant
et chaque pixel voisin. Près des bords la définition du
contraste est beaucoup plus délicate car le voisinage
défini est incomplet tandis que l’image doit rester de
taille identique et que la l’addition se fait pixel à
pixel.
Le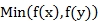 
et
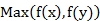intervenant dans la définition du contraste
sont fonction du niveau d’éclairement de
référence.
- Ces contrastes permettent de déterminer de
nouvelles méthodes de segmentations
d'images:
Pour chaque niveau de gris k, on procède
à un seuillage de l'image à k. On calcule ensuite le
contraste associé à chaque frontière extraite. On
construit ainsi une fonction de l'ensemble des niveaux de gris dans
R+. Les maxima locaux de cette fonction déterminent les seuils
séparant au mieux les classes de radiométrie de
l'image.
- La seconde application consiste en la
construction de cartes de contraste : le niveau de gris chaque
pixel x de l'image est remplacé par le contraste local en ce
point. Ce traitement permet, entre autre de mettre en évidence
les contours des objets.
Le modèle LIP
est bien adapté àl'extraction d'objets clairs sur un fond
clair ou d'objets sombres sur un fond sombre
1. Image numérique
