Reconnaissance de
formes
LES MOMENTS
INVARIANTS
Entrées/Sorties
Image binaire >> Affichage des
résultats dans trois
fenêtres :
-
une image
dans laquelle apparaissent les axes d’inerties (centré
sur le point de gravité)
-
une dans
laquelle les formes sont numérotées.
-
un
listing contenant les valeurs des paramètres cités
ci-dessous et des 7 moments pour chaque forme.
Méthode & paramètres
calculés
Les moments sont
utilisés pour associer le niveau de gris d’un point de
l’image à la masse d’un corps en chaque point. On
peut reprendre le même formalisme dans le cas d’un objet
binaire. Les différents moments fournissent des informations
importantes concernant l’arrangement spatial des points de
l’objet.
Equation des
moments : 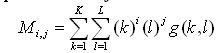
où g(k,l) est le niveau
de gris de l’image défini pour l=1..L
et k=1..K
Dans le cas d’une image binaire,
g(k,l)= 0 si on est sur une forme et 255 sinon.
Dans ce cas, le moment M0,0
représente la surfacede la forme
considérée.
Ces moments engendrent des moments invariants par
rotation :
M1 =
µ02+µ20
M2 =
(µ02-µ20)² +
4*µ11²
M3 =
(µ30-µ12)² +
(3µ21-µ03)
M4 =
(µ30+µ12)² +
(3µ21+µ03)²
M5 = (µ30 –
3µ12)( µ30 +
3µ12)[(
µ30+µ12)²-3(µ21+µ
03)²] + (µ21 –
3µ03)( µ21 +
3µ03)[(
µ30+µ12)²-3(µ21+µ
03)²]
M6 =
(µ20 - µ02)[( µ30 +
µ12)²-(
µ21+µ03)²]+4µ11(µ
30+µ12)(
µ21+µ03)
M7 =
(3µ21-µ03)(
µ30+µ12)[(
µ30+µ12)²-3(µ21+µ
03)²]-( µ30-3µ12)(
µ21+µ03)[3(µ30+µ
12)²-(µ21+µ03)²]
Ces 7 descripteurs de l’objets permettent de
calculer de nombreux paramètres de formes. Voici ceux qui sont
implémentés.
Le
périmètre : il
calculé à l’aide de la distance euclidienne :
deux pixels côte à côte sont plus proches que deux
pixels en diagonale.
Calcul par ordonnancement des pixels du contour
puis addition des distances successives liant deux pixels
voisins.
L’élongation
d’une
forme
Résolution de l’équation du second
degré : -x2 + (a-b).x + c = 0 avec
a=µ20 , b=µ02 ,
c=µ11 .
E = | x1| / |x2| avec x1, x2 racines telles que
x1<x2.
Si E est proche de 1 il s’agit alors
plutôt d’une forme allongée.
Le
diamètre : il est
défini ici comme la plus grande distance entre deux points du
contour de la forme. Calcul à partir des points du
contour.
L’excentricité
: c’est
l’éloignement du centre de la forme par rapport au
contour.
e = |
( h20
– h02
)2 – 4* h11
|
La
rondeur : elle caractérise si une forme
se rapproche d’un disque.
Si la rondeur est proche de 1, la forme est ronde
sinon la forme s’éloigne d’une forme
circulaire. Rondeur
=4 π * Surface / Pec²
où Pec=
Périmètre_Enveloppe_Convexe
La
convexité : elle
caractérise si la forme est plus ou moins
convexe.
Plus elle est proche de 1, plus la forme est
convexe :
Convexité
= Pec / périmètre
La
compacité : elle
caractérise si la forme est plus ou moins
compact.
Plus elle est proche de 1, plus la forme est
convexe :
Compacité
= 4 π * Surface / Périmètre
²
Les axes
d’inerties : ils forment
un système de coordonnées qui minimise la variance de la
forme projetée sur chaque axe :
V(s,u) = uT T u où u est le
vecteur de l’axe de projection
et 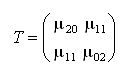
A partir de la matrice T, on peut ainsi calculer
les deux axes d’inertie u1 et u2
correspondant aux vecteurs propres de la matrice
T.
 1. Image numérique
1. Image numérique

