=>Dimensionnement \ Méthodes analytiques \ Elastoplastique \ Convergence-confinement

Théorie

* Principe général
* Hypothèses
* Courbe de convergence
* Courbe de confinement

 

1)Principe général

Considérons une section plane d'un terrain dans lequel on souhaite creuser une galerie circulaire. Ce terrain est soumis à une contrainte naturelle correspondant à un état initial isotrope P. Le déplacement radial u des parois de la galerie non encore excavée est évidemment nul.

•Pour modéliser l'excavation de la galerie, nous supposons d'abord la cavité remplie d'un liquide à une pression Pi correspondant à l'état initial isotrope P.

•Comportement du massif

Ensuite, en diminuant la pression Pi, on provoque un déplacement radial u correspondant à la décompression du massif. Cette pression Pi est diminué depuis la valeur P jusqu'à la pression nulle. Dans un premier temps, le comportement du terrain est élastique linéaire et la courbe de pression déplacement est linéaire du point A au point B. Dans un second temps, lorsque le critère de résistance du matériau du massif est atteint sur les parois de la cavités, une zone décomprimée apparaît autour du tunnel. Elle s'étend vers l'intérieur du massif au fur et à mesure que la pression Pi décroît. C'est la portion BC de la courbe. La courbe ABC est appelée courbe caractéristique du massif excavé.

•Comportement du soutènement

Avec le même système d'axes, nous pouvons aussi représenter le déplacement radial du soutènement en fonction de la pression extérieure Pi qui lui est appliquée. Sa courbe caractéristique est une droite si nous supposons que son comportement est élastique linéaire. Son origine est décalée de la valeur us0 pour tenir compte de la convergence qui s'est déjà produite lors de sa mise en place.

•L'équilibre final,
qui permet de déterminer la pression de soutènement, est obtenu en superposant les deux courbes caractéristiques sur un même graphique. Le point d'intersection i définit alors le point d'équilibre.

2)Hypothèses

L'utilisation de développements analytiques, telle que dans la méthode de convergence-confinement, pour dimensionner les soutènements des ouvrages souterrains impose une réduction du nombre de facteurs à prendre en considération. En effet, la méthode de convergence-confinement est une méthode de calcul simple mais suffisante dans bien des cas. Elle sacrifie la géométrie de l'ouvrage, l'anisotropie du comportement mécanique du massif, l'anisotropie des contraintes pour tenir compte de facteurs jugés plus importants sur l'équilibre final. Ainsi, l'hypothèse de l'axisymétrie a été faite.

Les conditions suivantes doivent alors être remplies :

• Le tunnel est de section circulaire

• Le matériau est composé d'un matériau homogène et isotrope

• Le champ de contraintes initiales est hydrostatique. C'est-à-dire que les contraintes naturelles verticale et horizontale sont égales

• Le tunnel est suffisamment profond pour que l'on puisse négliger la variation de la contrainte initiale hydrostatique à sa proximité

• Le soutènement est supposé exercer une pression radiale uniforme sur les parois de l'excavation

D'autre part, pour que l'on puisse étudier le problème en état plan de déformation, la longueur du tunnel sera suffisamment importante. La déformation longitudinale sera alors considérée comme nulle.

 

•Comportement du massif

Pour dessiner la courbe de convergence du massif et pour le calcul des contraintes et déplacements, un grand nombre de solutions analytiques ont été proposées. Les différentes approches dépendent du critère de rupture du massif, du comportement post-rupture du massif et de la manière de considérer les déformations dans cette phase. Les critères de rupture les plus utilisés sont ceux de Tresca, de Mohr-Coulomb et de Hoek & Brown.

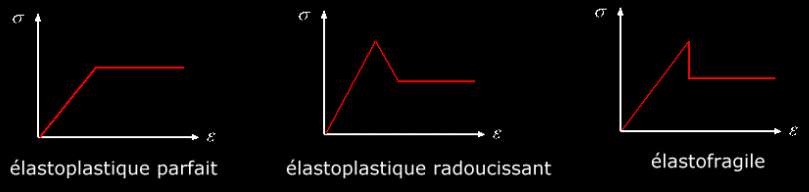
Au-delà de la phase élastique, lorsque le seuil de résistance du massif est atteint, on peut généralement distinguer trois types de modélisations du comportement du massif :

• élastoplastique parfait
• élastoplastique radoucissant
• élastofragile



D'autre part, il convient de définir les lois de déformation lors de la rupture. De nombreuses approches ont été envisagées. Rappellons, par exemple, la loi où l'on suppose une relation linéaire entre les variations des déformations radiale et tangientielle (Panet & Gaudin, 1976; Panet, 1976) :

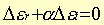
avec 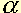coefficient de dilatance

3) Courbe de convergence

Notations utilisées

Les calculs par la méthode de convergence-confinement sont basés sur les relations suivantes (Corbetta, 1990) :

• Equation d'équilibre :

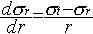
• Equations de comportement :

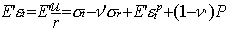
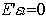
Avec

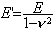et

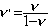Pour obtenir les solutions analytiques de trois types de comportement du massif cliquez sur les liens:

• Comportement du massif qui reste élastique jusqu'à la fin du chargement,

• Comportement du massif où une plastification apparaît pour un matériau élastoplastique parfait

• Comportement d'un massif élastoplastique radoucissant.

Ces solutions explicites sont présentés pour le critère de rupture de Mohr-Coulomb :

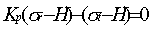
et la loi de déformation plastique suivante (Panet & Gaudin, 1976; Panet, 1976) :

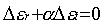
soit une relation linéaire entre les variations des déformations radiales et tangentielles

 

4) Courbe de confinement

Pour tracer la courbe de confinement ou la courbe de caractéristique du soutènement, on détermine trois valeurs :

1) La raideur du soutènement :

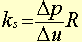
où	p, pression exercée sur le soutènement
	u, le déplacement radial correspondant
	R, rayon de l'excavation

2) La pression maximale admissible 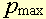. Elle correspond à la rupture du soutènement.

3) La convergence initiale 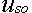. Le soutènement étant placé alors qu'un certain déplacement radial du massif s'est déjà produit. On introduit en général la notion de taux de déconfinement .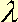

Considérons trois types de soutènement :

• Soutènement en béton projeté ou en béton coffré

• Soutènement par cintres calés à la paroi

• Soutènement par boulons à ancrage ponctuel

Pour obtenir la raideur et la pression maximale de chacun il vous suffit de cliquer sur le lien voulu