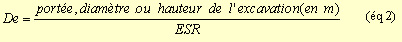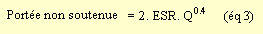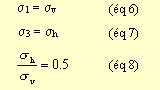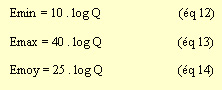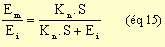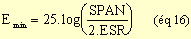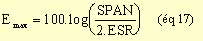Théorie

où

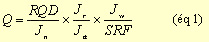
-RQD est le Rock Quality Designation de Deere. -Jn est l'expression du nombre de familles principales de discontinuités. -Jr caractérise la rugosité des faces des joints. -Ja définit le degré d'altération des joints (épaisseur dujoint et nature du matériau de remplissage). -Jw spécifie les conditions hydrogéologiques : importance des venues d'eau et pression. -SRF (Stress Reduction Factor) précise l'état des contraintes dans le massif.

Barton & Al donnent les commentaires suivants, qui permettent d'expliquer le regroupement des paramètres par paire:

L'indice Q peut varier de 0.001 à 1000. Les Q sont regroupés en 9 classes.Chaque classe correspond à une qualité de massif rocheux (cf. tableau ci dessous).
Les classes de Q se représentent sur une échelle logarithmique.

Contrairement à la classification de Bieniawski, le Q-system a connu très peu de modifications depuis sa publication.
Les seuls changements ont eu lieu au niveau du paramètre SRF avec un changement de valeur dans le cas de roches compétentes et sous de très fortes contraintes.

Barton a proposé une relation empirique donnant la portée maximale (en mètres) en deçà de laquelle la cavité peut rester stable sans soutènement:

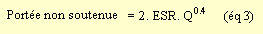
Lorsque la portée d'une excavation excède la portée limite prédite par l'équation ci-dessus, il est nécessaire d'installer un système de soutènement en vue de maintenir le massif rocheux entourant l'excavation dans des conditions acceptables de stabilité. En 1974, Barton, Lien et Lunde ont proposé 38 catégories de support (à base de boulonnage, de béton projeté, de revêtement en béton, ou de toute autre combinaison de ces types de renforcement) en fonction des paramètres Q et de De.

Le graphique représentant les 38 classes de soutènement est représenté ici .

On y retrouve également la zone stable sans soutènement délimitée par l'équation 3. (voir).
Ces catégories sont déterminées à l'aide de la valeur de Q, et du quotient De.
Les soutènements sont ensuite déterminés en fonction de la classe de soutènement et à l'intérieur de cette classe à partir des valeurs de sous paramètres comme (RQD/Jn), (Ja/Jr) et (De).

Les techniques de soutènement ont évolué depuis 1974. Au début les techniques utilisées étaient le boulonnage local, le boulonnage systématique, le béton projeté par voie sèche accompagné de treillis soudés, et du revêtement en béton coffré.
Vers 1993 le graphique représentant les différentes classes de soutènements a été modifié : les 38 classes ont été remplacées par des catégories plus vastes, et les techniques nouvelles ont été introduites.

En effet, le béton projeté par voie humide et le béton projeté avec fibres d'acier ont remplacé le béton projeté associé au treillis soudé existant. Le boulonnage local, le boulonnage systématique et les revêtements en béton coffré sont toujours utilisés.

2.Détermination des efforts

La valeur de l'indice Q est utilisée dans le calcul de la pression qui s'exerce sur le soutènement. Au niveau de la voûte la pression s'exprime de la façon suivante :

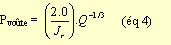
Cette équation peut être améliorée avec l'introduction du paramètre Jn et l'équation (4) est remplacée par l'équation (5) :

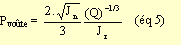
On remarque que les équations (4) et (5) sont équivalentes quand le massif rocheux présente 3 familles de discontinuités.
Quand il y a moins de trois familles de discontinuités l'équation (5) donne une valeur inférieure à celle donnée par l'équation (4), et quand il y a plus de trois familles de discontinuités c'est l'inverse.
Au niveau de la paroi, des observations ont montré que la pression qui s'exerce sur le soutènement est égale au tiers de la pression qui s'exerce au niveau de la voûte, en supposant un état de contrainte "normal" :

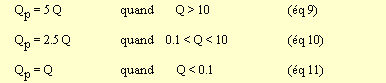
Un nouvel indice Qp est recalculé. Il correspond à l'indice Q mais au niveau des piedroits et se nomme "Wall quality" ou "indice de qualité au niveau des piédroits". La valeur de Qp se calcule à partir de Q :

Pour obtenir la pression exercée sur le soutènement au niveau des piedroits on introduit Qp dans les équations (4) et (5).

3.Détermination du module de déformabilité du massif.

Le Q-system permet de calculer le module de déformabilité du massif.
Pour un même massif rocheux il existe trois valeurs de module de déformabilité : un module minimum (Emin), un module maximum (Emax) et un module moyen (Emoy).
Ces 3 modules peuvent être calculés à l'aide de l'indice Q:

Barton présente aussi la formule ci-après qui permet de calculer Em à partir de l'espacement des discontinuités (S), de la raideur normale des joints (Kn) et du module de déformabilité de la roche intacte (Ei) :

La raideur normale des joints Kn est la pente de la droite n = f(Vn), où n est la contrainte normale et Vn la déformation normale équivalente, lors d'une essai de serrage.

Toutes les formules précédentes permettent de calculer Em dans le cas d'excavation avec soutènement. Pour des excavations sans soutènement le module de déformabilité est calculé à l'aide de la largeur de l'excavation (SPAN) et du coefficient ESR

4.Détermination de la vitesse des ondes P

Certaines personnes utilisent l'indice Q pour calculer la vitesse des ondes P. (cf. référence bibliographique 4)

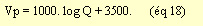
Retour à l'introduction