|
=>Reconnaissance \ essai in situ \ Méthodes géophysiques \ Gravimétrie \ |
||
Description des principes de bases de ces méthodesIntroduction : Nous rappelerons la loi de la gravitation, puis nous expliquerons les paramètres qui vont influencer les valeurs de g mesurées (altitude, rotation de la Terre, forme de la Terre, présence d'autres masses extérieures à la Terre, présence latérale de masses importantes en surface de la terre, présence de masses sous la surface de la Terre, isostasie). Et pour finir nous décrirons le mode opératoire utilisé pour cette famille [45]. Rappel : la loi d'attraction universelle des corps. 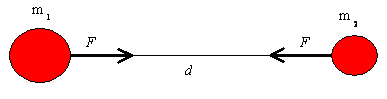
L'interaction de gravitation est une attraction qui est proportionnelle à la masse des deux corps et inversement proportionnelle au carré des distances. 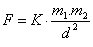
Cette force qui exprime l'interaction de gravitation est dirigée du centre de gravité du premier corps au centre de gravité du second. La force d'interaction entre les deux corps est identique, en d'autres termes la force appliquée à m1 est identique à la force appliquée à m2. En mécanique classique, non relativiste, la masse inerte et la masse dynamique sont identiques. Donc, cette force s'exprime aussi par le produit de la masse du corps par son accélération. Soit : F= m.a Comme la force d'interaction entre les deux corps est identique, leurs accélérations seront inversement proportionnelles à leurs masses respectives. Cette force de gravitation détermine entièrement les mouvements des corps célestes, mais aussi les corps observables à la surface du sol : il n'y a pas de différence fondamentale entre le déplacement d'un ballon de football rebondissant sur le pied d'un joueur et le déplacement d'une planète autour du système solaire. Paramètres affectant l'attraction de la pesanteur "g" : L'altitude : Cette distance qui n'est autre que la somme de l'altitude et du rayon de la Terre au point d'observation doit donc être prise en compte dans la détermination de la valeur locale de l'attraction de la pesanteur. A une altitude quelconque (supposée positive) il faut ajouter un terme positif pour retrouver la valeur nominale de l'attraction de la pesanteur à l'altitude zéro. C'est la correction d'altitude ou correction à l'air libre. La rotation de la Terre : Le fait que la terre tourne sur elle-même provoque une accélération tangentielle qui se compose avec l'attraction de la Terre pour la réduire quelque peu. Cette accélération est nulle aux pôles et maximale à l'équateur. La forme de la Terre : La Terre a la forme d'un ellipsoïde aplati aux pôles. La distance par rapport au centre de la terre étant plus faible aux pôles, l'attraction y est plus forte qu'à l'équateur. On a ainsi pu calculer un géoïde qui détermine ce que devrait être l'attraction de la pesanteur en tenant compte de la forme réelle de la Terre et de la vitesse de rotation de la Terre (ce deuxième terme étant nettement moins important que le premier). Cette valeur est appelée par convention G0. Il existe plusieurs géoïdes convenant plus ou moins à telle ou telle zone géographique ou à telle profession. La présence d'autres masses extérieures à la Terre :
Une mesure gravimétrique doit donc être corrigée de la double influence de la lune et du soleil; c'est la correction luni-solaire, dépendant de l'heure de la mesure. La présence latérale de masses importantes en surface de la Terre, à proximité du point d'observation : Toujours en fonction de la distance et de leur masse, la présence de reliefs importants va modifier localement l'attraction de la pesanteur. Si on cherche à éliminer ces masses, on applique la correction de relief. La présence de masses plus ou moins importantes sous la surface de la Terre : La correction d'altitude ne tient compte en effet que de la distance au centre de la Terre ; il faut aussi tenir compte de l'attraction due au fait que, sous le point d'observation il y a un terrain de densité connue qui attire l'observateur et diminue donc la correction d'altitude ou correction à l'air libre. C'est ce qu'on appelle la correction de densité L'isostasie atteinte ou non par la région : On remarque lors de mesures répétées que l'excès de masse rencontré au droit d'une montagne est compensé par un déficit de masse en dessous. Cette quasi-constance de l'attraction de la pesanteur au-dessus des massifs continentaux et des mers exprime l'isostasie, c'est-à-dire le principe de l'équilibre de la croûte terrestre sur la partie supérieure du manteau; c'est l'hypothèse d'Airy. Longtemps mise en doute, elle compare la croûte terrestre à un iceberg de densité 2,7 flottant sur un liquide de densité 3,1. Autrement dit, cela signifie que l'excès de masse rencontré au droit d'une montagne est compensé par un déficit de masse en dessous. Il ne faut pas en conclure que la correction de densité ne doit pas être prise en compte ; c'est uniquement à l'échelle du globe que l'isostasie joue un rôle, pas à une échelle locale. A cette échelle plus locale, tous les phénomènes géologiques mettant en jeu des variations de masse spécifique provoquent des variations de l'attraction de la pesanteur. Ordre de grandeur des corrections:
Méthode de mesure : 

Exemple de résultat : 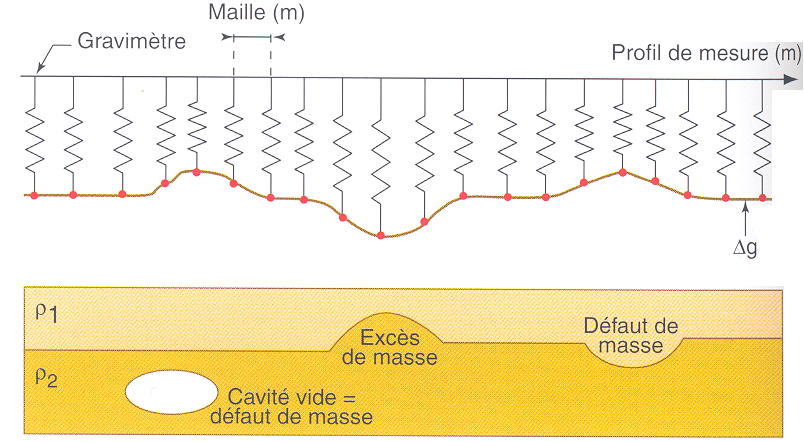 Source : [48] Exemples de méthodes (gravimétrie) Retour à la Gravimétrie |