Partenaires :







=>Reconnaissance \ essai in situ \ Méthodes géophysiques \ Sismique \


Notions théoriques



Les notions fondamentales que le doit connaître en sismique sont : (un rappel sur les pertes est fait à la fin).

Type de milieu étudié


La sismique n'est que la propagation du champ de contrainte à l'intérieur d'une structure (sol, roche, ouvrage d'art).
On peut tout aussi justement dire que c'est la propagation du champ de déformation.
Cela implique de faire des hypothèses sur le matériau constitutif de la structure pour décrire de la manière la plus adéquate le milieu dans lequel l'onde se propage.

Milieu élastique-linéaire


En première approximation, on peut considérer le sol comme un milieu élastique-linéaire.

La mécanique théorique montre que les corps solides présentent des comportements différents suivant l'intensité des forces extérieures qui tentent de les déformer. Dans le domaine des petites déformations, le modèle élastique est largement applicable à la plus grande gamme des solides habituellement rencontrés.
Le plus simple des modèles élastiques est le modèle élastique linéaire, homogène et isotrope :
  • l'élasticité exprime qu'il y a un rapport bi-univoque entre la contrainte exercée sur un corps et sa déformation;
  • la linéarité exprime que pour une contrainte déterminée la déformation d'un corps élastique est directement proportionnelle à cette contrainte;
  • l'homogénéité exprime qu'en tout point du corps ce rapport contrainte-déformation ne change pas, ce qui ne signifie nullement qu'il est le même dans toutes les directions;
  • l'isotropie exprime que ce rapport est indépendant de la direction.

Une des caractéristiques du comportement élastique est que lorsque l'on retire la contrainte appliquée le corps revient dans son état initial. Du fait de la linéarité, on peut appliquer le principe de superposition, c'est-à-dire que les différentes déformations s'additionnent linéairement pour obtenir une déformation totale. On peut représenter le modèle élastique par un ressort linéaire qui se déforme d'une manière directement proportionnelle à la force exercée et qui reprend sa forme initiale lorsqu'on enlève cette force.

Cette approximation est d'autant plus intéressante, si on ne désire pas tenir compte des phénomènes dissipatifs, par la relative simplicité des équations qui en découlent.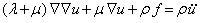

Formule d'équilibre volumique d'un milieu élastique linéaire
Où :
λ et μ sont les paramètres de Lamé;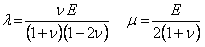
Formule qui relie les paramètre de Lamé à E et coef de poisson.
E est le module de Young;
ν est le coef de poisson;
ρ est la densité du matériau;
f sont les forces de volume;
u est le vecteur déplacement.


Type d'ondes rencontrées


Si on cherche les solutions de ses équations, on remarque qu'il y en a de deux grands types :
  • les ondes de volume;
  • les ondes de surface.
Les solutions sous forme d'ondes de volume existent toujours, mais les ondes de surface nécessitent que si l'on rajoute une interface qui limite le milieu (c'est sur cette interface que vont apparaître les ondes de surface).

Les ondes de volume


Les ondes de volume sont de deux types les ondes de compression (onde P) et les ondes de cisaillement (onde S).

Représentation des ondes P :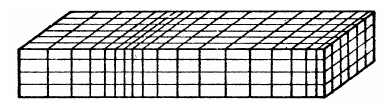
Représentation des ondes 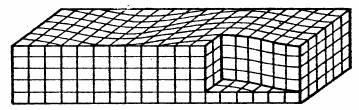de compression

Représentation des ondes S :
Représentation des ondes de cisaillement

Leurs vitesses dépendent des caractéristiques du milieu et valent :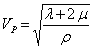
Vitesse des ondes de compression pour les ondes de compression.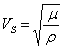
Vitesse des ondes de cisaillement pour les ondes de cisaillement.
Leur rapport vaut : 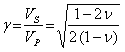rapport des vitesses de compression et de cisaillement, or ν est compris entre 0 et 0.5, cela implique que VP>VS.

Les ondes de surface


On peut trouver un autre type de solution si on rajoute deux hypothèses à l'équation d'équilibre :
  • recherche d'une solution de forme exponentielle,
  • on limite le domaine à un demi-espace (on introduit alors, qu'il n'y a pas de contraintes à la surface libre de ce demi-espace).
Ce rajout permet de trouver les ondes de surface qui sont de deux types :

onde Rayleigh :
Représentation des ondes de Rayleigh

et onde de Love :
Représentation des ondes de Love

La vitesse des ondes de Rayleigh est reliée à la vitesse des ondes de cisaillement par :
Vitesse des ondes de Rayleigh
Ce qui nous donne que VS>VR.

Les pertes et la répartition de l'énergie d'un choc


A titre indicatif voici un tableau qui donne la répartition de l'énergie en fonction du type de l'onde.

Type de l'onde % de l'énergie total
Onde de surface 67
Onde de cisaillement 26
Onde de compression 7

Si on ne regarde que l'interface du milieu (le sol), les ondes perdent petit à petit leur énergie.
Cette perte dépend de la nature de l'ondes, pour les ondes de volume elle diminue comme r2 et pour les ondes de surface elle diminue comme r-1/2.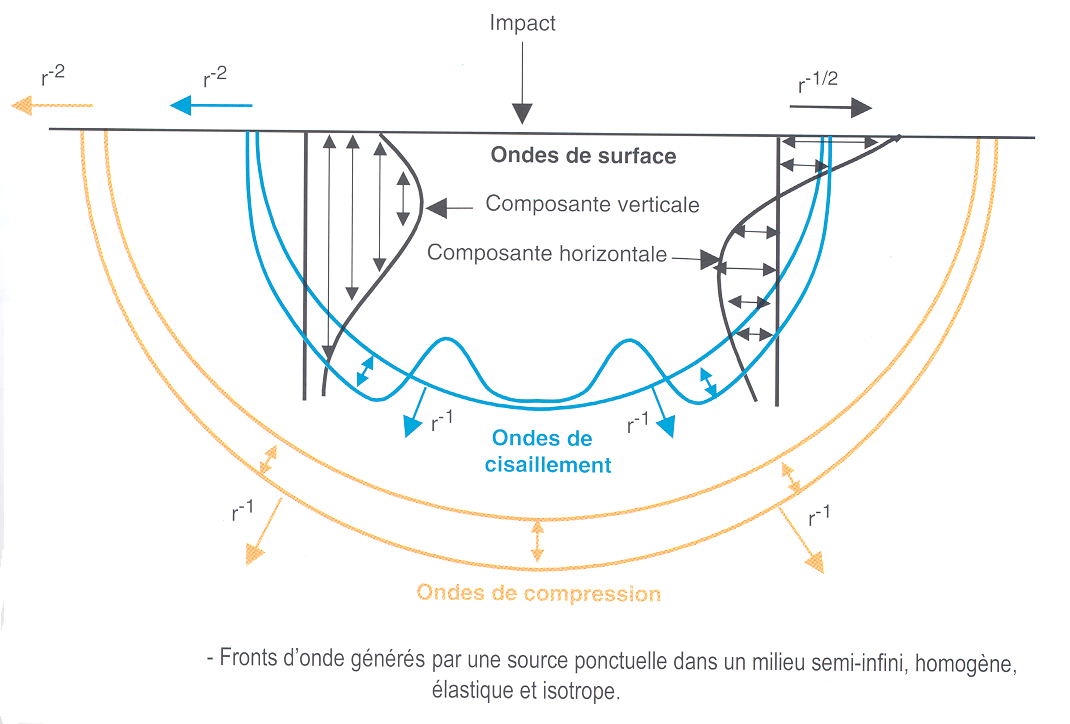
Les pertes d'énergies des ondes sismiques
Source : [48].

Description des principes de bases de la sismique

Exemples de méthodes (Sismiques)

Retour à la Sismique