Théorie
* Hypothèses
* Principe
1° Hypothèses
* les
joints sont des discontinuités naturelles planes que l'on peut
clairement individualiser,
* les blocs découpés
par les joints et les surfaces de l'ouvrage sont supposées rigides,
* les contraintes
agissant sur le pourtour de l'ouvrage ne sont pas susceptibles de provoquer
de nouvelles fissures par dépassement de la résistance
de la matrice rocheuse.
2° Principe
L'analyse de Goodman se déroule en 3 étapes:
*
Description des joints
*
Détermination des keyblocks
*
Stabilité et effort à reprendre
1) Description des joints
Pour décrire géométriquement un
joint, il faut spécifier son inclinaison et sa direction d'inclinaison.
|
Figure 1: Description d'une faille
Ces joints par leurs combinaisons vont décrire
tous les blocs du massif et de ce fait tous les blocs présent
à la périphérie de l'excavation. Il faut également
déterminer les angles de frictions de ces joints.
2) Analyse géométrique:
Détermination des Keyblocks
1.Principe du Keyblock
Seul les blocs les plus critiquement orientés
et de type finis (c-à-d dont le volume est bien défini
dans les limites du domaine étudié) situés à
la périphérie de l'excavation, doivent être supportés.
S'ils sont stables (soit grâce à un système de support,
soit grâce à la friction le long des faces du bloc) alors
les blocs situés derrière eux resteront en place. [4]
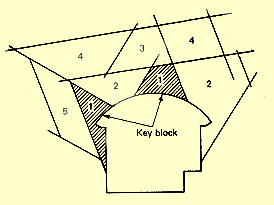 |
Figure 1: Illustration du principe du Keyblock
Extrait de [6]
2. Determination des Keyblocks
Deux moyens sont possibles pour déterminer les
Keyblocks et leurs positions parmis tous les blocs décrits par
les joints soit :
* la projection stéréographique
* la méthode des vecteurs
3)Analyse de la stabilité
et des efforts à reprendre
Ayant identifié un keyblock et sa position, il
est possible de calculer son poids et d' entamer une analyse de stabilité.
1. solution 3D d'un Keyblock situé dans le plafond
du tunnel
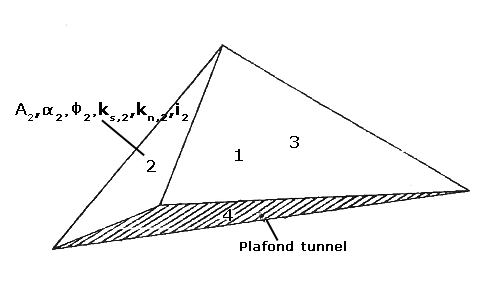 |
Figure 2: étude en 3 dimensions
* contraintes
initiales: Il faut tenir compte des contraintes initiales qui sont stabilisatrices
dans le cas étudié :
| |
|
σ1,0;σ2,0:contrainte
maximale et minimale dans le plan 4 de la figure
αi: angle complémentaire de l'inclinaison
Θp,i:direction par rapport au nord de σ1,0,
σ2,0
Θi:direction d'inclinaison
|
* proportion du poids
à reprendre par le soutènement:
| |
|
A0/W: proportion du poids du bloc à
reprendre
W: poids du bloc
Ai:aire de la face i du bloc
αi: angle complémentaire de l'inclinaison
de la face i
ks,i:rigidité tangentielle de la face i
kn,i:rigidité normale de la face i
Φi:angle de friction de la face i
ii: angle de rugosité de la face i |
2. solution 2D
Voici une simplification du problème en 2D:
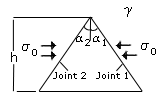 |
Situation 2D
Goodman propose les expressions suivantes:
| |
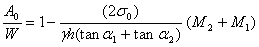 |
|
A0: force du support vertical
W: poids du Keyblock
σ0:contraintes initiales
α: angle complémentaire de l'inclinaison
γ: poids volumique du sol
h: hauteur jusqu'à l'intersection des 2 joints |
et
| |
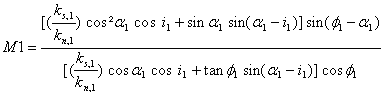
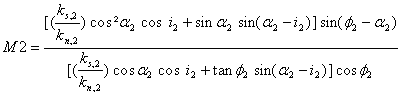
|
|
ks:rigidité tangentielle
kn:rigidité normale
Φ:angle de friction du joint
i: angle de rugosité du joint |
| |
|